[알고리즘] 주어진 정수 N 까지의 소수 구하기 (시간복잡도&제너레이터)

[시간복잡도 O(N^2)]

일반함수 버전

const isPrimeNumber = (number) =>{
    for (let i =2; i <=number/2; i++){
        if(number % i == 0){
            return false
        }
    }
    return true;
}

function getAllPrimeNumbers(number) {
    let primeNumbers = [];
    for (let i=2; i<=number; i++){
        if(isPrimeNumber(i)) primeNumbers.push(i)
    }
    return primeNumbers;
}

console.log(getAllPrimeNumbers(23))

[실행결과]

 

제너레이터 버전

function* genAllPrimeNumbers(number) {
    for(let i=2; i<=number; i++) {
        if(isPrimeNumber(i)) yield i;
    }
}

let primeNumberGeneroater = genAllPrimeNumbers(7);
console.log(primeNumberGeneroater.next())
console.log(primeNumberGeneroater.next())
console.log(primeNumberGeneroater.next())
console.log(primeNumberGeneroater.next())
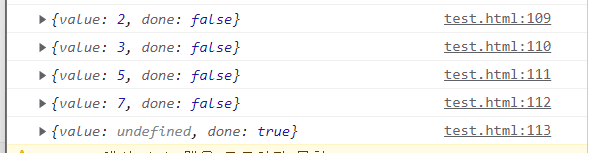
console.log(primeNumberGeneroater.next())

[실행결과]

 

 

[시간복잡도 O(N * log(log(N)) + M)]

일반함수 버전

Q1) 왜 i를 sqrt(n)만큼(루트 N)도는것인가?

A1) 소수는 2부터 쭉 올라가면서 배수를 없애가는 작업이라고 생각할 수 있다. (2의배수들 지우고 -> 3의 배수들 지우고 ->4의 배수들 지우고... ) 즉 숫자 a를 하나씩 증가시키면서 a의 배수들을 순서대로 지운다. 그럼 숫자 a를 언제까지 올리는가? 가장 최적의 방법을 생각한 것이 바로 루트 n이다. n = p*q라고 표현될 때, p는 항상 루트n 이하이고, q는 항상 루트n 이상이기 때문에, 루트n 까지만 돌면 된다!

function getPrimes(n) {
    let primeBool = new Array(n+1).fill(1);
    primeBool[0] = primeBool[1] = 0

    i = 2
    while(i<= Math.sqrt(n)){
        if(primeBool[i]){
            j = i*i
            while(j<=n) {
                primeBool[j] = 0
                j = j+i
            }
        }
        i++
    }
    
    res = []
    for (let i = 0; i<=n; i++){
        if(primeBool[i]){
            res.push(i)
        }
    }

    console.log(res)
}

getPrimes(20)

[실행결과]

 

제너레이터 버전

function* getPrimes(n) {
    let primeBool = new Array(n+1).fill(1);
    primeBool[0] = primeBool[1] = 0

    i = 2
    while(i<= Math.sqrt(n)){
        if(primeBool[i]){
            j = i*i
            while(j<=n) {
                primeBool[j] = 0
                j = j+i
            }
        }
        i++
    }

    res = []
    for (let i = 0; i<=n; i++){
        if(primeBool[i]){
            yield i
        }
    }
}

let priemGen = getPrimes(20);

console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())
console.log(priemGen.next())

[실행결과]